Ding:Spiro
| Foto | |
|---|---|
| |
| Basisdaten | |
| Status | funktionstüchtig |
| Schöpfer | Papageier (Diskussion) |
Inkscape-Datei zum Download: Medium:Spiro-komplett.svg
Outline
Der Spiro ist ein Einsteigerprojekt für den Lasercutter, das relativ schnell zu ersten greifbaren Ergebnissen führt und anschlienßend Schritt für Schritt Techniken vorstellt, um diese Ergebnisse zu verbessern, bis am Ende ein komplexes Spielzeug im Steampunk-Style dabei heraus kommt.
Was ist das Ziel?
Der Spiro ist ein Werk-/Spielzeug, mit dem man mittels Stift und Papier komplexe, regelmäßige Muster malen kann. Er besteht aus einer Anzahl von Schablonen und einem zugehörigen Zeichenrahmen und ist von ähnlichen, seit Jahrzehnten kommerziell erhältlichen Kinderspielzeugen inspiriert. Rahmen und Schablonen greifen dabei wie Zahnräder ineinander, ein Stift verfolgt die Umlaufbahnen einer Schablone und hinterlässt eine entsprechende Spur auf dem Papier. Allerdings macht es natürlich viel mehr Spaß, sich dieses Spielzeug selbst zu basteln und weiter zu entwickeln.
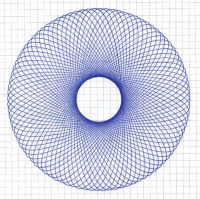
Die Ergebnisse können, wenn mehrere Schablonen und Stifte verwendet werden, farbenprächtig und komplex sein; aber auch mit nur einem Stift und einer Schablone sind schon beeindruckende Muster möglich. Hier ist ein Beispiel:
Solche und ähnliche schöne Muster lassen sich mit freier Hand kaum herstellen. In Zeiten von leistungsfähigen Grafikprogrammen und erschwinglichen Farblaserdruckern ließen sie sich natürlich mit relativ wenig Aufwand auf elektronischem Wege erzeugen - aber auch wenn das Ergebnis optisch perfekt erscheint - die Faszination des Spirogramms ist eine andere. Sie liegt gerade in der großen Einfachheit der Mittel - Papier, Stift und Zahnrad - und des Prozesses, der den simplen mathematischen und mechanischen Gesetzen eines Getriebes folgt. Nicht umsonst wurde der Spiro ursprünglich als Kinderspielzeug bekannt: um mit dem Spiro faszinierend perfekte Muster zu zeichnen, ist kaum künstlerisches Talent nötig; ein wenig Übung genügt.
Was brauchen wir?
Wir werden unseren Spiro als Schnittvorlage für den Lasercutter anfertigen. Die Laserfertigung bringt uns die notwendige Präzision und erleichtert die Arbeit erheblich . Wir brauchen also den Lasercutter und geeignetes Material (ich empfehle 3mm MDF oder Acryl). Für den fertigen Spiro werden wir eine ganze Platte (40x30cm) benötigen, für Prototypen genügen vorhandene Reststücke.
Für die Herstellung der Vorlage verwenden wir Inkscape, ein frei verfügbares Vektor-Zeichenprogramm, das es für alle gängigen Plattformen gibt. Der Gestaltung der Zahnräder sind kaum Grenzen gesetzt; schöne Vorlagen gibt es beispielsweise in der freien Vektorgrafik-Bibliothek von openclipart.org. Das Projekt setzt erste Erfahrungen im Umgang mit dem Lasercutter voraus; außerdem sollte die grundsätzliche Verwendung von Inkscape bekannt sein (Formen anlegen, Größe und Drehwinkel ändern, Füllung und Konturlienien bearbeiten, Objekte ausrichten und gruppieren etc.). Die spezielleren Funktionen für die Gestaltung der Zahnräder werden erklärt.
Ein wenig Theorie
Der Spiro basiert mathematisch auf rationalen Zahlen, also dem Divisionsverhältnis zweier positiver Ganzzahlen, die durch die Anzahl der Zähne zweier Zahnräder repräsentiert werden. Das eine Zahnrad läuft in einem Getriebe um das andere herum (wobei letzteres fest mit der Unterlage verbunden ist). Dabei gibt der Kehrwert des Bruchs aus dem Zahnzahlen (äußeres im Zähler, inneres im Nenner) die Anzahl der Umdrehungen des äußeren Zahnrads je Umlauf um das innere an, die Nachkommastellen liefern die Anzahl der benötigten Umläufe, bis die Zahnräder wieder in ihrer ursprünglichen Position zueinander zum Stehen kommen. Sehen wir uns ein Beispiel an. Nehmen wir an, das innere Zahnrad hat 30 Zähne und das äußere 27. Der Wert für diese Kombination von Zahnrädern ist also
x = 27/30 = 9/10 = 0,9
Der Kehrwert des Bruchs beträgt dann
1/x = 10/9 = 1,1
Das äußere Rad dreht sich also bei jedem Umlauf um das innere 1,¯1 mal um sich selbst. Um die Anzahl der benötigten Umläufe um das innere Rad zu bestimmen, bis beide Zahnräder wieder ihre ursprüngliche Position zueinander eingenommen haben, verwenden wir folgende Formel:
y = 1/(|1-x|) = 1/0,1 = 10
Nach 10 Umläufen stehen die beiden Zahnräder wieder in ihrer ursprünglichen Position. Würde man einen Punkt auf dem äußeren Zahnrad verfolgen, käme er nach 10 Umdrehungen wieder an seinem Ausgangspunkt an. Zeichnet man seine Bewegung dabei auf - zum Beispiel indem man an dieser Stelle ein Loch durch das Zahnrad bohrt und einen Stift hindurch steckt - dann entsteht eine Bahn, die sich nach 10 Umdrehungen selbst überdeckt. Und genau das tun wir mit dem Spiro.
Hätte das äußere Zahnrad 29 Zähne, hätte x den Wert 0,96 und y den Wert 30; das Muster wäre also erst nach 30 Umdrehungen geschlossen (und damit wesentlich komplexer). Ähnlich sähe es auch aus, wenn das äußere Zahnrad größer wäre als das innere, etwa mit 31 Zähnen: dann hätte x den Wert 1,03 und y läge ebenfalls bei 30. Man erkennt: je näher die Zahlen beieinander liegen und je größer sie dabei sind, desto komplexer wird das Muster. Zudem scheint es offensichtlich sinnvoll zu sein, teilerfremde Zahnzahlen zu verwenden . Bei der Konstruktion unseres Spiro werden wir uns daran orientieren.
Ein Wort über Zahnräder
Für den Spiro benötigen wir in erster Linie Zahnräder; oder zumindest etwas, was so ähnlich aussieht. Die Konstruktion von guten Zahnrädern ist eine Wissenschaft für sich. Wer's nicht glaubt, frage einen engagierten Ingenieur - man nehme sich aber Zeit, der resultierende Vortrag kann unter Umständen länglich ausfallen. Ein Wirtschaftsinformatiker, der über die Konstruktion von Zahnrädern spricht, kann nur Unfug erzählen. Deswegen werden wir keine Zahnräder konstruieren, sondern nur so tun als ob. Glücklicherweise wird das Ergebnis trotzdem ähnlich funktionieren wie echte Zahnräder - und für unsere Zwecke völlig ausreichen.
Damit unsere Zahnräder gut ineinander greifen und sich problemlos umlaufen können, müssen sie ein paar grundlegende Eigenschaften aufweisen. Zunächst sollten die Zähne auf allen Rädern gleich breit und tief sein. Sind sie ungleich breit, greifen sie nicht ineinander; bei ungleichmäßiger Tiefe hat das Getriebe Spielraum und "wackelt". Da der Spiro kaum Kraft übertragen muss, verwenden wir einfache, dreieckig zulaufende Zähne mit einer leichten Abrundung an der Spitze (die sowohl die Verletzungsgefahr vermindert als auch ein Abbrechen der Zahnspitzen vermeidet).
Nachdem die Zähne gleiche Breite und Tiefe haben sollen, ist die Anzahl der Zähne direkt proportional zum Umfang des Rades, und damit auch zum Radius. Anders ausgedrückt: Ein Zahnrad mit doppelt so vielen Zähnen hat auch doppelt so viel Umfang und doppelt so großen Radius wie das Vergleichsstück. Das wird uns die Konstruktion der verschiedenen Zahnradgrößen relativ einfach machen.
Anleitung
Bevor es losgeht
In den folgenden Kapiteln werden Schritt für Schritt die Einzelteile des Spiro entstehen. Dabei werden ganz bewusst auch ein paar Teile zum Ausprobieren konstruiert und ausgeschnitten, die später nicht mehr benötigt werden. Es macht also nichts, wenn mal eine Konstruktion nicht passt oder ein Schnitt misslingt. Fehler sind dazu da, um daraus zu lernen.
Auf geht's
Der einfachste denkbare Spiro braucht eigentlich nicht mehr als zwei Zahnräder. Eins davon sollte irgendwo ein Loch haben, durch das man den Stift stecken kann. Und genau damit fangen wir an. Aber wie konstruiert man ein Zahnrad in Inkscape? Schauen wir mal.
Schritt 1: Der Stern
In erster Näherung ist ein Zahnrad nichts weiter als ein Kreis mit Zacken an der Außenlinie. Man könnte auch sagen: ein Stern mit vielen und zu kurzen Spitzen. Inkscape hat ein Stern-Werkzeug, das solche generierten Sterne unterstützt - probieren wir's doch mal aus.
- Starte Inkscape und lege ein neues Dokument an; die Seitengröße spielt im Moment noch keine Rolle.
- Aktiviere das Stern/Polygon-Werkzeug
- Schalte die Stern-Option an
- Stelle die Anzahl der Ecken auf 24
- Stelle das Spitzenverhältnis auf 0,840 ein
- Stelle die Abrundung auf 0,200 ein
- Lass die Zufallsänderung auf 0,000 eingestellt.
- Ziehe mit der Maus einen Stern auf - die Größe ist erst mal unwichtig.
- Schalte um auf das Anfasserwerkzeug
- Schalte die Kombination von Breiten- und Höheneinstellung ein
- Ändere die Größe des Sterns auf 48mm.
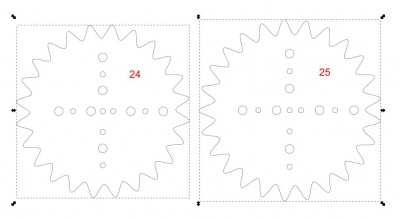
Jetzt haben wir schon mal ein erstes Zahnrad (im Bild schon mit ein paar Zeichenlöchern):
Nachdem wir ein schön komplexes Muster haben wollen, wählen wir für das zweite eine Zahnanzahl möglichst nah am ersten - sagen wir: 25.
Um dieses Zahnrad zu konstruieren können wir genauso vorgehen wir beim ersten - nur dass die Zahnanzahl diesmal natürlich 25 betragen muss. Außerdem muss das Zahnrad etwas größer werden als das letzte. Wie schon erwähnt ist praktischerweise die Zahnanzahl direkt proportional zum Umfang und damit zum Durchmesser des Rades. Wenn die Zahnanzahl von 24 auf 25 steigt (also auf 25/24 der ursprünglichen Anzahl), dann muss auch der Durchmesser auf 25/24 des ursprünglichen Durchmessers steigen. In unserem Fall hat das neue Rad daher 50mm Durchmesser (statt 48mm).
Das gleiche Ergebnis lässt sich übrigens auch erzielen, indem man das ursprüngliche Rad kopiert (Strg-D oder Strg-C + Strg-V), die Größe auf 50mm ändert und mit dem Stern-Werkzeug die Anzahl der Ecken auf 25 erhöht.
Probieren wir's aus:
- Positioniere die beiden Zahnräder nebeneinander links oben auf der Seite
- Stelle sicher, dass die Linienstärke bei beiden 0,01mm beträgt (Strg-Shift-F), damit der Laser entlang der Linien schneidet.
- Speichere das Projekt (als SVG)
- Speichere eine Kopie als PDF
- Bring das PDF zum Laser und lass es aus einem passenden Reststück ausschneiden
Et voilá: Zwei Zahnräder.
Schnapp Dir einen Bohrer (2mm) und mach ins das größere Zahnrad ein kleines Loch (egal wo, nur nicht zu nah an der Mitte) um später den Stift hindurch zu stecken. Jetzt kannst Du das kleinere Zahnrad auf ein Stück Papier legen (Tip: Festhalten reicht, aber besser geht's mit einem Tropfen Kleber oder ein paar Stecknadeln und einer Korkmatte drunter; Du kannst für die Stecknadeln auch noch Löcher ins kleinere Zahnrad machen) und ausprobieren, ob das größere Rad sauber außenherum läuft. Wenn ja, stecke einen Stift durch das Loch im größeren Rad und lass es um das kleine Rad laufen, bis die Spur geschlossen ist. Unsere Formel von oben sagt:
x=25/24; y=1/(|1-x|) = 24
Nach 24 Umrundungen müsste die Spur also geschlossen sein. Probier's aus! Das Ergebnis müsste etwa so aussehen:
BILD
Schritt 2: Sterne und Schwarze Löcher
Gut. Bisher haben wir zwei Zahnräder - und die Erfahrung, dass es ziemlich umständlich ist, damit Muster zu zeichnen. Außerdem gibt es bis jetzt nur ein einziges Muster. Im zweiten Schritt wollen wir das ändern.
Als erstes sorgen wir mal für mehr Mustervielfalt, will sagen: für mehr Löcher. Natürlich könnte man wieder den Bohrer aktivieren - aber wozu? Wir haben einen Laser, der kann das gleich mit erledigen. Alles was dazu nötig ist, sind ein paar kleine Kreise. In Inkscape:
- Aktiviere das Kreis-Werkzeug
- Halte die Strg-Taste gedrückt
- Ziehe mit der Maus einen Kreis auf; die Größe ist egal.
- Aktiviere das Anfasser-Werkzeug
- Schalte die Kombination von Breiten- und Höheneinstellung ein
- Ändere die Größe des Kreises auf 1,5mm
Die Größe von 1,5mm passt am besten für Feinminenstifte und Fineliner. Wenn Du lieber Blei- oder Buntstifte verwenden möchtest, nimm 2,0 - 2,5mm Kreisdurchmesser. Unter 1,5mm kann der Laser nicht zuverlässig ausschneiden, über 2,5mm hat der Stift Spiel und das Muster wird ungleichmäßig. Du kannst mehrere Kreise mit unterschiedlichem Duchmesser auf dem Zahnrad anbringen; dann kannst Du später frei zwischen den Stiften wählen. Weiter gehts:
- Fertige einige Kopien des Kreises an (Strg-D oder Strg-C + Strg-V)
- Verteile die Kopien an unterschiedlichen Stellen der beiden Zahnräder; einige weiter innen, andere weiter außen, so dass die entstehenden Muster unterschiedlich groß werden.
- Wenn Du möchtest, nutze die Ausrichten-Funktion (Strg-Shift-A) von Inkscape, um die Kreise gleichmäßig anzuordnen.
Damit haben wir schon wesentlich mehr Muster zur Verfügung.
Als nächstes konstruieren wir noch mehr Zahnräder mit unterschiedlichen Zahnzahlen. Hier sind die Werte für ein paar weitere Zahnradgrößen :
| Zähne | Durchmesser | s |
|---|---|---|
| 22 | 44mm | 0,825 |
| 24 | 48mm | 0,840 |
| 25 | 50mm | 0,846 |
| 27 | 54mm | 0,857 |
| 29 | 58mm | 0,867 |
| 33 | 66mm | 0,883 |
| 37 | 74mm | 0,896 |
| 39 | 78mm | 0,901 |
| 47 | 94mm | 0,918 |
| 92 | 184mm | 0,957 |
Bei 24 und 25 Zähnen konnten wir das Verhältnis von Innenkreis zum Spitzenkranz ("Spitzenverhältnis") noch unverändert lassen; die Werte liegen nah genug beieinander. Wenn wir uns daran machen, deutlich größere und kleinere Zahnräder zu konstruieren, werden wir diesen Wert anpassen müssen - aus dem einfachen Grund, dass die Zähne der Räder gleich hoch bleiben müssen, das Spitzenverhältnis aber relativ zum Radius angegeben ist. Damit ändert sich die absolute Zahntiefe automatisch, wenn wir den Radius ändern. Um passende Zähne zu konstruieren, müssen wir also die das Spitzenverhältnis anpassen. Das kann man empirisch machen (durch Ineinanderschieben der konstruierten Zahnräder auf dem Bildschirm), oder mathematisch. Die Zahnhöhe h bei Durchmesser D und Spitzenverhältnis s ist (für unser ursprüngliches Zahnrad mit 24 Zähnen und 48mm Durchmesser):
h=((1-s)∙D)/2=((1-0,840)∙48mm)/2=3,84mm
Umgekehrt lässt sich daraus für jeden Durchmesser D das passende Spitzenverhältnis s ausrechnen:
2h=(1-s)∙D s=(1-2h)/D
Die Werte passenden Werte für s sind in der Tabelle mit aufgeführt.
Auch auf diesen Zahnrädern können beliebig viele Stiftlöcher angebracht werden. Am besten funktionieren übrigens Löcher, die weder zu nah am Rand sind (wo es teilweise schwierig wird, das Rad sauber weiter zu drehen) noch zu nah an der Mitte (wo das Muster zu einem ganz flachen Band zusammenfällt). Die aufgeführten Zahlen sind entweder teilerfremd oder lassen sich nur auf teilerfremde Brüche kürzen, so dass wir keine doppelten Muster im Set haben.
Schritt 3: Den Dingen einen Rahmen geben
Jetzt fehlt nur noch ein bequemerer Weg, die Muster zu zeichnen - ohne jedes Mal ein Zahnrad auf dem Papier befestigen zu müssen. Dazu fertigen wir uns einen Zahnrahmen, sozusagen ein inverses Zahnrad. Glücklicherweise funktioniert die Mathematik in diesem Fall genau wie für "echte" Zahnräder, so dass wir die Konstruktionsmethode fast unverändert lassen können.
Der Rahmen kann natürlich so groß sein, wie Du ihn haben willst - ich nehme für den Anfang einfach die gängigste Papiergröße (A4) als Maßstab. Als erstes brauchen wir ein Quadrat in der Größe der Seitenbreite einer A4-Seite - das sind 21cm.
- Aktiviere das Rechteck-Werkzeug
- Halte die Strg-Taste gedrückt
- Ziehe mit der Maus ein Quadrat auf; die Größe ist erst mal egal.
- Aktiviere das Anfasser-Werkzeug
- Schalte die Kombination von Breiten- und Höheneinstellung ein
- Ändere die Größe des Quadrats auf 210mm
Als nächstes tricksen wir ein bisschen: Wir raten geschickt, dass 92 Zähne bei 180mm Durchmesser eine gute Größe für das Zahnrad auf der Rahmen-Innenseite sein könnte (man kann das auch ausrechnen). Das Zahnrad zu konstruieren und in der Mitte des Quadrats zu platzieren, sollte jetzt kein Problem mehr sein.
So langsam müssen wir uns aber ein paar Gedanken um den Platz auf dem Werkstück machen. Fangen wir mal beim Maximum an: der Laser kann Werkstücke von 40x30cm bearbeiten; in dieser Größe gibt es auch passende Materialplatten. Es bietet sich daher an, in Inkscape die Seitengröße auf dieses Maß einzustellen. Im Menü Datei-->Dokumenteinstellungen finden sich die Seitenmaße. Stelle das Format auf Querformat ein, lege die Seitengröße im Bereich Benutzerdefiniert mit 400x300mm fest, und stelle auch die Standard-Einheiten auf Millimeter ein.
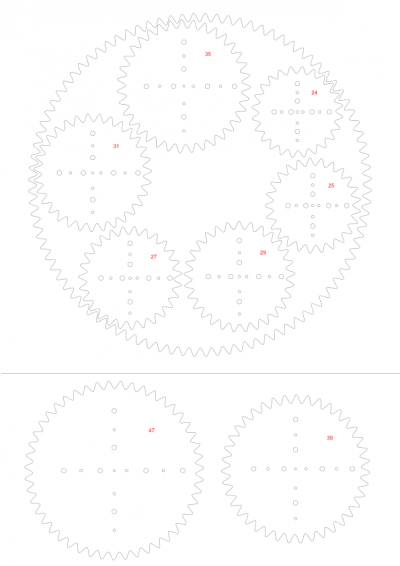
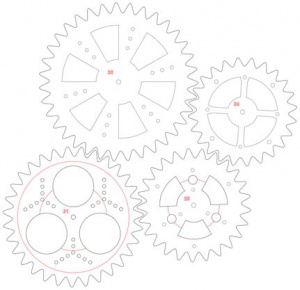
Gruppiere das Quadrat mit dem großen Zahnrad (Strg-G) und platziere es links oben auf der Seite. Um Material zu sparen, positionieren wir die Zahnräder innerhalb des großen Zahnrades - der Innenteil wäre sonst Verschnitt. Gruppiere jedes Zahnrad mit den Löchern, die Du darauf positioniert hast, und schiebe sie in den Rahmen: die Zahnräder 24-25-29-27-31-35 passen in dieser Reihenfolge zusammen in den Innenkreis. Die beiden großen Zahnräder (39 und 47) sollten noch unter den Rahmen passen. Damit ist die halbe Materialplatte ausgefüllt - auf der zweiten Hälfte könnte man nun noch eine zweite Kopie unterbringen - oder noch mehr große Zahnräder. So könnte das zum Beispiel aussehen (die ausgeschnittenen Zahnräder sind rechts zu sehen):
Schritt 4: Verzierungen
Die fertigen Zahnräder und den Rahmen kann man natürlich färben und lackieren, wie Geschmack und Material es zulassen (MDF eignet sich dazu wesentlich besser als Acryl). Aber auch hier kann man den Laser einsetzen, um Verzierungen anzubringen. Dafür gibt es im Wesentlichen drei Möglichkeiten:
- Rastern: der Laser kann beliebige Bilder (die sich als Bitmaps in Inkscape importieren lassen) auf die Oberfläche der Zahnräder brennen. Dazu arbeitet der Laser wie ein Nadeldrucker und brennt kleine Löcher in die Oberfläche, wo sich die Struktur (bzw. Farbe) verändern soll. Acryl ist für diese Methode nur bedingt geeignet.
- Schneiden: neben den notwendigen Formen können zusätzliche Ornamente angebracht und vom Laser ausgeschnitten werden. Diese Methode eignet sich zum Beispiel hervorragend, um die unten gezeigte Steampunk Variante des Spiro zu realisieren.
- Brennen: mit dem Laser können Linien nicht nur geschnitten, sondern auch als Linienzug in die Oberfläche gebrannt werden. Dazu wird der Laser aus seinem Fokuspunkt heraus gefahren, so dass die Energie nicht mehr ausreicht, um das Material zu schneiden; stattdessen wird es lediglich verkohlt bzw. verschmort.
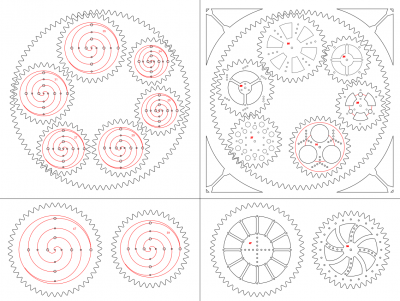
Der Phantasie sind bei den Verzierungen eigentlich kaum Grenzen gesetzt. Meinen ersten Spiro habe ich zum Beispiel mit Spirallinien (Inkscape: Spiral-Werkzeug) versehen, und die Löcher für die Stifte entlang der Spiralen platziert. Nachdem ich zwei Spiralen ineinander gezeichnet habe, hatte ich Platz für zwei verschiedene Lochgrößen.
Wichtig: Wenn im gleichen Projekt 0,01mm-Linienzüge für Schneiden und Brennen gleichzeitig auftauchen, hilft die Color Mapping Funktion des Lasers. Die Details finden sich im Wiki und in der Anleitung des Herstellers, aber in aller Kürze verhält es sich so, dass schwarze 0,01mm-Linien immer geschnitten werden (zumindest wenn der Vector-Modus aktiviert ist), farbige Linien aber nur dann, wenn Color Mapping nicht aktiviert ist. Mit Color Mapping kann ich jeder Farbe einen bestimmten Betriebsmodus des Lasers zuordnen - zum Beispiel Schneiden bei verändertem Fokus. Wenn die Verzierungen z.B. in Rot gehalten sind und ich der Farbe Rot den Modus Schneiden mit +500 Fokus-Einstellung zuordne, werden rote Linien mit abgesenktem Objekttisch geschnitten - was de facto dazu führt, dass die Linien nur eingebrannt werden.
Wenn man mit Inkscape und der Verarbeitung von Pfaden etwas vertrauter geworden ist , kann man extrem filigrane Ornamente realisieren - von Steampunk bis zu orientalischer Architektur, von floralen Motiven bis Klöppelmustern ist alles denkbar. Wenn dabei etwas hübsches heraus kommt - denk daran, es zu veröffentlichen. Hier sind zwei Beispiele, mit eingebrannten Spiralmustern und als ausgeschnittenes Steampunk-Design:
Alternativen
Inkscape bietet neben der Sterne-Funktion noch andere Möglichkeiten, Zahnräder zu konstruieren. Einige davon will ich hier anreißen (und begründen, warum ich sie nicht verwende).
Alternative 1: Cliparts
Aus diversen Quellen (wie openclipart.org) sind Vektorgrafiken von Zahnrädern aller Art verfügbar und können legal für private Zwecke verwendet werden. Auf den ersten Blick ist das eine gute Alternative, weil man sich die ganze Konstruktionsarbeit spart. Allerdings ist man in der Regel auf den vorhandenen Satz an Elementen beschränkt: wenn neue und andere Zahnräder hinzu kommen sollen, gibt es keine passende Konstruktionsanleitung, und einfach Skalieren hilft bei Zahnrädern leider nicht (sie würden nicht funktionieren). Deswegen "drehe ich selber".
Alternative 2: Pfadeffekt "Zahnrad"
Inkscape selbst kennt Pfadeffekte (Menü Pfad-->Pfad-Effekte), die jedem beliebigen Pfad zugewiesen werden können. Einer dieser Effekte ist "Zahnrad". Dieser Effekt erzeugt je nach Ausgangspfad ein oder mehrere Zahnräder unterschiedlicher Größe. Auch diese Alternative erscheint auf den ersten Blick überzeugend (gerade weil die Räder sich per Mausklick anpassen lassen). Auch dieser Effekt hat leider gravierende Nachteile.
Zum einen lassen sich die Zahnräder nur begrenzt gut trennen; man kann den Effekt wiederum in einen Pfad umwandeln (Menü Pfad-->Objekt in Pfad umwandeln) und dann die einzelnen Räder verwenden. Allerdings lassen sie sich anschließend nicht mehr ohne weiteres verändern.
Zum anderen sind die berechneten Zahnräder nur begrenzt funktionstüchtig. Sie arbeiten zwar mit Zapfen und Flanken und sind damit den oben beschriebenen "Sternen-Zahnrädern" theoretisch überlegen. Leider ist die Berechnung nicht genau genug, die entstehenden Zahnräder drehen sich nur mühsam, so dass der Spiro keinen Spaß mehr macht.
Alternative 3: Render-Erweiterung "Zahnrad"
Dies ist eine echte Alternative zum "Sternen-Zahnrad". Die Funktion im Menü Erweiterungen --> Rendern --> Zahnrad bietet die Möglichkeit, mechanisch taugliche Zahnräder mit Zapfen und Flanken zu berechnen und dabei automatisch die richtige Größe zu erzeugen. Insofern kann ich diese Alternative durchaus empfehlen. Sie hat einen kleinen Vorteil, dafür auch zwei kleine Nachteile gegenüber den "Sternen-Zahnrädern".
Der erste Nachteil besteht darin, dass sich auch hier die Größe nachträglich nicht mehr ändern lässt. Wenn das Zahnrad nicht passt, muss ein neues erzeugt werden. Der weite kleine Nachteil besteht darin, dass die Kreisteilung nur in Pixel angegeben werden kann, was für Laserprojekte keine geeignete Größe ist. Beide Nachteile lassen sich aber mit etwas Übung bzw. Kompromissen umgehen.
Der Vorteil besteht darin, dass sich neue Zahnräder sehr schnell erstellen lassen. Außerdem ist diese Art Zahnrad etwas stabiler gegen Abrutschen, die entstehenden Getriebe laufen daher etwas "runder". Ob man den Unterschied spürt und welche Methode man bevorzugt, sei jedem selbst überlassen.
Update: Es gibt eine neuere Version dieser Erweiterung, die mir noch unbekannt war. Dazu gibt es auch eine eigene Wikiseite.